Chapter 01 정보의 시각화
1. PIE Chart
- 차이가 없으면 시각적 효과가 떨어짐.
- 최대값 100%로 이상인 경우 시각적으로 넓이가 맞지 않음.
2. Bar Chart
- 막대가 하나의 범주. 도수를 나타냄(혹은 퍼센트 값)
- 수직/수평 막대 그래프.
3. 히스토그램
- 구간별 도수 값을 시각화
- 바 사이가 벌어져있지 않고 붙어있는 것으로 보임.(범위니까!) - 하지만 진짜 붙어있진 않지..
- 구간이 일정치 않을 수 있지만, 막대 면적의 합은 전체 도수의 합과 같아야 함.
- 막대의 높이는 단위 막대 길이당 도수의 값. 높이 = 도수/막대길이(가로)
- 누적 도수를 그래프로 그릴 수 있음.
Chapter 02. 데이터의 중심 경향
1. 평균 : Sum (시그마, 서메이션) X / n (뮤 μ 라고도 함)
2. 중앙값 : 이상치(Outlier)가 있는 경우 평균값이 너무 커진다(왜곡시킨다).
- 편향된 데이터 skewed data
- 오른쪽으로 편향된 데이터 skewed to the right . 왼쪽으로 편향된 데이터 skewed to the left : 꼬리가 긴쪽을 편향되었다고 표현. (이상치들이 존재하니까!)
- 좌우 대칭 데이터 symmetric data
- 중앙값(중간값) median과 평균
3. 최빈값 : 극단에 있는 값들이 몰려 있는 경우 일부 값 수정에 따라 중간값이 크게 바뀔 수 있음. 도수 분포표로 표현하면 어디에 분포가 몰려있는지 확인 가능. 이 경우 mode 최빈값을 구한다.
Chapter 03. 변이와 분포 측정하기
1. 범위 range : 평균과 더불어 확인해야 함. 하한과 상한의 간격을 범위라고 함.
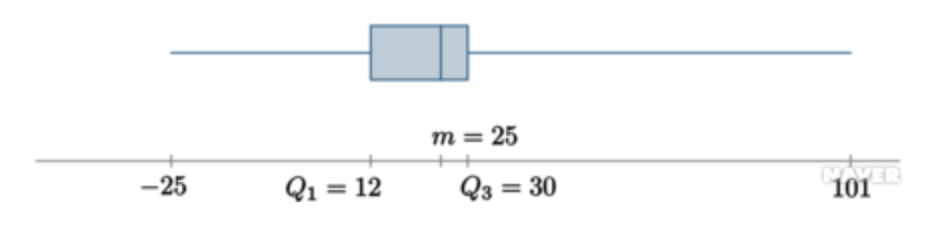
2. 사분위 : 이상치 존재시 범위를 확인하면 데이터가 어떤지 정확하게 인식하기 어려움. 사분위는 Q1(lower quuartile), Q2(median), Q3(upper quartile), Q4로 나눠서 사분위수로 표현.
- 사분범위 Q3 - Q1 : 작은 범위 만듬. 이상치를 잘라낸 모양이라고 판단.
3. 십분위, 백분위 : 십분위수, 백분위수 (K%) : 상대적인 값을 의미 Pk
4. 박스플랏
5. 분산과 표준편차
- 평균으로부터 각 데이터 거리(편차)를 제곱으로 해서 더하고 갯수를 나눔(평균으로 만듬)
= 편차 제곱의 평균 : 분산
- 분산에 루트를 씌운것 : 표준편차 : 단위를 기존 데이터와 같게 만들기
6. 표준점수 (표준화)
- 표준점수는 평균을 0으로 만드는 것. (값-평균)/표준편차
- 서로 다른 평균의 데이터를 비교하려 할 때
Chapter 04. 확률 계산하기
1. 확률 : 사건A가 일어나는 갯수 / 전체 사건 갯수
- 벤다이어그램으로 시각화 가능.
- 사건이 일어나는 경우 + 일어나지 않을 확률(여사건) = 1(전체 확률)
- 확률은 더할 수 있다. 둘 사이에 겹치는 경우가 없을 경우에는. (배반사건)
2. 확률의 덧셈 : 둘 사이에 겹치는 경우가 있는 경우 확률을 더하고 동시에 일어나는 경우(교집합)를 한 번 빼면 됨.
- 교집합 기호와 합집합 기호 (알지?)
3. 조건부 확률 : 어떤 상황(조건)에서 하의 확률 : P(A|B) = 동시에 일어나는 경우(교집합) / (조건 내)전체 경우
- 확률 트리 (나눠지는 루트(분기)에서는 반드시 배반사건이어야 함)

4. 베이즈 정리와 독립사건 (Monday:A, Tuesday:B)
- P(B) = P(A ∩ B) + P(\A_'_ ∩ B) : B 전체 집합은 A, B가 동시에 일어나는 경우와 A 여집합, B가 동시에 일어나는 경우의 합이다.
- 그 속에 교집합들의 확률은 P(A ∩ B) = P(A) X P(B | A) : A의 전체 확률에 B사건 하의 A의 조건부 확률을 곱한 값.
- 결론) P(B) = P(A) X P(B | A) + P(A') X P(B | A') : 전확률의 법칙
- 베이즈 정리 : 모든 경우의 수 확률을 모를 때 P(B | A)에서 P(A | B)를 구하는 유용한 방법.

- P(A | B) = ( P(A) X P(B | A) ) / ( P(A) X P(B | A) + P(A') X P(B | A') )
- 독립사건일때, 두 사건은 조건부 확률에 영향을 주지 않음. 두 사건 확률을 곱하면 P(A ∩ B)와 같음.
Chapter 05. 이산확률분포
1. 슬롯머신의 확률
2. 이산확률분포 : 값이 정해져 있는, 셀 수 있는 확률의 분포
- 기대치 : 평균값

- 기대치를 이산확률분포에서 구하기 : 변수와 확률값을 곱해주고 다 더해주면 됨.
- 분산 : ((확률변수-기대치)^2)와 확률값을 곱해주고 다 더해주면 됨.
- 표준편차 : 분산^1/2

3. 확률의 선형관계
- 두 확률의 변수가 선형관계에 있는 경우분산은 Var(aX+b) = a^2Var(X)으로 구할 수 있다.
- 기댓값은 E(aX+b) = aE(X) + b
- 공분산 : 두 확률변수의 분포가 결합될 때 그 결합 확률 분포의 분산을 측정하는 것으로 Cov(X, Y)로 표현

- 공분산이 0인 것은 두 확률 변수 사이에 비례적 선형관계를 발견할 수 없는 경우
- 비례 관계 정도에 따라 공분산 크기 바뀜
- 서로 영향 없는 경우에 사건, 결과로 나타날 값은 관측값, 매번 새롭게 독립관측. 두 확률 변수가 독립관측인 경우, 기댓값은 각각의 기댓값을 더해주면 됨. 사건의 뺄셈을 한 경우에는 기댓값을 빼줘야 됨.
- 분산은 각각의 분산을 더해주면 됨. (독립일때만!!!) 사건 뺄셈 한 경우 분산을 더한값과 같음 (제곱했기때문에...)
<예제>

Chapter 06. 순열과 조합
1. 팩토리얼 : 전체 경우의 수 구할 때 n! = n * (n-1) * (n-2) * ... * 1
- 원 모양 배치에서는 한 말을 고정하기 때문에 (n-1)!
2. 순열
: N 가지의 경우에서 n개를 뽑는 경우의 수 (순서를 생각하는 경우) : N! / (N-n)! : 결과적으로는 N개부터 하나씩 줄어들면서 뽑는 수 만큼 곱하면 됨.
3. 조합
: N 가지 경우에서 n개를 뽑는 경우의 수 (순서를 생각하지 않는 경우) : N! / (n! * (N-n)!) : 결과적으로는 N개부터 하나씩 줄어들면서 뽑는 수 만큼 곱한 값에 n!을 나누면 됨.
Chapter 07. 기하, 이항, 푸아송 분포
1. 기하분포 : 성공확률 p, 실패확률 q=1-p / r-1번 실패하고 1번 성공함 : P(X=r) = (q^(r-1)) * p
- 기하 분포의 최빈값은 1
- P(X > r) = q^r
- P(X <= r) = 1-q^r
- 성공을 거둘 확률이 p 일때 변수 X가 기하분포를 따른다 : X~Geo(p)
- 기댓값 : 성공률 누계 (P(X <= r))는 (1/성공률)에 수렴 (ex. 성공률 0.2라면 5에 수렴)
- 분산 : q 실패확률 / p^2 성공확률의 제곱
2. 이항분포 : 보기 ?개(확률값 계산)인 질문 n개에 대해 정답을 구하는 확률 : 베르누이 시행

- P(X = r) = nCr * p^r * q^(n-r)
- 기하분포와 이항분포의 차이
- 이항분포는 성공의 수에 관심. 기하분포는 성공을 거두기 위해 시행해야 하는 시행의 횟수에 관심.
- 이항분포는 n번 시행해서 성공적인 결과를 얻는 수를 X라고 할 때, r번의 성이 있을 확률을 구하는 것.
- 기하분포는 변수 X가 첫번째 성공(사건이 일어나는 것)을 거두기 전 까지 시도해야하는 시행의 횟수.
- X가 이항분포를 따를 때, p의 확률일 때 n번 시행인 경우 : X ~ B(n, p)
- 기댓값 : (한번 시행시) p (n번 시행시) n*p
- 분산 : (한번 시행시) p*q (n번 시행시) n*p*q

3. 포아송 분포 : 어떤 주어진 구간에 사건이 발생하는 수를 X라고 하고, X가 구간마다 람다(발생 수의 평균값)만큼 발생하는 푸아송 분포.
- X ~ Po(λ)
- 특정 구간에 r번 발생이 있을 확률은 P(X=r) = (e^(-λ)*λ^r) / r!
- 기댓값, 분산 : λ
- 푸아송 분포는 람다가 커질수록 람다를 기준으로 좌우대칭으로 생긴다.
Chapter 08. 정규분포
1. 연속데이터 : 이산데이터는 정확한 값을 취한다. 연속확률변수들이 갖는 확률분포를 설명하기 위해 확률밀도함수를 사용할 수 있음.
2. 확률밀도함수의 전체 면적은 1. 그러므로 f(x)의 확률밀도함수 구할 수 있음.
- 연속확률분포에서 확률을 구하는 방법은 확률밀도함수의 면적을 계산하는 것과 같음.
3. 정규분포와 표준정규분포
- 자연적인 데이터들은 대부분 정규분포를 따른다.
- 정규분포는 연속데이터를 위한 이상적인 모델이다.
- x ~ M(u, 시그마^2)
- 확률테이블을 통해 면적을 계산함. = 표준정규분포에 대해서 제공.=> z = (X - u) / (시그마)
- => N(0, 1) 평균이 0이고 분산이 1인 표준 정규분포. 표준화 한다고 표현함.
- 확률테이블은 ~보다 작을 확률을 제공해줌. 확률분포 그림에서 해당 범위 전부분!!
4. 두 개의 정규분포 합치기
- 두 확률변수가 독립이면 그냥 더해주고 빼도됨, 분산도 더해주고 빼주면 됨.
=> 두 독립된 변수라면 더해주면 됨. X + Y ~ N (평균합, 분산합)
5. 정규분포의 선형관계 및 독립관측
- 관계가 있는 경우.. 선형 관계를 이용하기 : aX + b ~ N (au + b, a^2*(시그마)^2)
- 독립관측의 경우 x1 + x2 + ... + xn : ~ N(xu, n*(시그마)^2)
6. 이항분포의 정규화
- 일반적으로 nq와 np가 모두 5보다 클 때 정규분포를 이항분포로 개략적으로 대체할 수 있다.
7. 연속성보정 : 정규분포와 이항분포는 다름. 이항분포가 많아지면 대체할 수 있다고 했지만 보정이 필요함.
- 연속성 보정을 통해서 구체적인 점수를 지정해서 확률 계산가능. (예시 참고)
8. 정규분포를 이용해서 푸아송분포 근사화하기
- 푸아송분포의 람다값이 작으면 좌우 대칭이 아니라서 정규분포로 근사화할 수 없음. 람다가 15 이상은 돼야함.
- 연속성보정 값으로 표준 점수를 구하면 됨.
'데이터 어쩌구 > 통계 ・ 수학' 카테고리의 다른 글
| [이론] 기초 : 모집단과 표본 (0) | 2021.10.26 |
|---|---|
| [Python 통계] chapter 14 군집분석 (0) | 2021.10.05 |
| [이론] 기초 수학 (0) | 2021.09.28 |
| [Python 통계] chapter 13 분류예측분석 (0) | 2021.09.26 |
| [Python 통계] chapter 12 요인분석 (0) | 2021.09.26 |
