1. 데이터 전처리 : 데이터 생성, 정제, 변환, 결합
1) 결측값 처리법
(1) 완전 제거법 (정보 손실의 분석 결과 왜곡 가능성 있음)
(2) 평균대체법 (추정량 표준오차가 과소 추정될 수 있음)
(3) 핫덱대체법 : 동일한 데이터 내 결측값이 발생한 관찰치와 유사한 특성을 가진 다른 관찰치의 정보를 이용하여 대체하는 방법
2) 이상치 판별
(1) 박스플롯 그려서 이외 Q1-1.5*IQR 과 Q3+1.5*IQR의 범위를 넘어가는 자료를 이상값으로 진단.
(2) 표준화 점수 (Z-score)의 절대값이 2, 3보다 큰 경우를 이상값으로 진단.
3) 이상값 처리
(1) 이상값 제외
(2) 이상값 대체 : 이상값을 정상 범위의 최소값, 최대값과 대체
(3) 변수 변환 : 자료값 전체에 로그변환, 제곱근 변환 등 적용.
4) 연속형 자료 범주화
(1) 방법 : 연속형 변수를 구간으로 이용해 범주화 하는 과정. 이상치 문제를 완화
(2) 효과 : 이상치 문제 완화. 결측치 처리 방법으로 사용. 분석시 과적합 방지 및 결과 해석 용이
5) 데이터 변환
(1) 목적 : 분포의 대칭화(정규화), 비슷한 산포(여러 그룹 비교할때)를 위해, 변수간 관계를 단순하게 만들기(비선형->선형으로) 위해 변환을 함.
(2) 유형
- 제곱근 변환 (왼쪽 꼬리 길게 만들어줌) vs 제곱 변환 (오른쪽 꼬리 길게 만들어줌)
- 로그 변환(왼쪽 꼬리 길게) vs 지수 변환(오른쪽 꼬리 길게)
- 박스콕스 변환 : 제곱근 유형의 변환 일반화, 제곱 유형의 변환 일반화

6) 데이터 결합 join : inner join, full outer join, left join, right join
2. 머신러닝
1) 개념 : 데이터를 스스로 학습시켜 문제를 해결할 수 있게 하는 기술.
2) 발전 : 머신러닝 알고리즘 발전 + 컴퓨팅 성능의 발전 + 대용량 데이터 축적 및 관리 기술 발전 = > 머신러닝의 활용 증가
3) 방법론 (분류)
| 지도학습 훈련용 데이터에서 여러 특성 변수를 이용해 목표변수를 예측하도록 모델을 학습함. |
회귀 알고리즘 목표변수(라벨)이 연속형 |
Linear Regrassion | Decision Tree SVM Random Forest Boosting Neural Network Deep Learning |
| 분류 알고리즘 목표변수(라벨)이 범주형 |
k-nearest Neighbors | ||
| Logistic Regression | |||
| Softmax regression | |||
| 비지도학습 = 자율학습 라벨 없는 훈련용 데이터에서 특징 변수들 간 관계나 유사성을 기반으로 의미있는 패턴을 추출. |
군집화 : 클러스터링 | k-means Clustering | |
| 차원축소 : 특성변수가 너무 많을때 | PCA | ||
| 추천시스템 | recommendation | ||
| 강화학습 : 행동 주체와 - 상태 - 보상이 - 바뀌는 환경 | SARSA, Q-Learning | ||
4) 분석 절차
(1) 주어진 데이터 전처리 탐색
(2) 적절한 모델을 선택
(3) 주어진 데이터로 모델을 훈련시킴
(4) 훈련된 모델을 적용해 새로운 데이터에 대한 예측을 수행
5) 검증 및 평가 : 어떻게 과대적합 문제를 막고 일반화 오차를 줄일 수 있을까
(1) Hold-out 방식 : 주어진 데이터를 Training 60%, (Validation 20%,) Test 데이터 20% 분류. 나누는 비율은 조정이 가능함
- 검증 데이터 Validation data : 훈련에 필요한 하이퍼파라미터를 조정하거나 변수 선택 등에 이용. 모델을 튜닝할 때 사용.
- 평가 지표를 활용해서 test, train 데이터를 비교. 두 데이터의 평가가 확연히 다른 경우(train이 훨씬 높은 경우) 제대로 훈련되지 않은 것임.
(2) k-fold 교차검증(Cross-validation) 방식 : 자료 수가 충분하지 않은 경우 훈련 데이터에서 많은 양을 소모하지 않도록 k개로 균등하게 분할하고 train(k-1), test(k)를 번갈아가면서 모델 훈련. 전체 다 반복하고 예측오차의 평균을 구함.

6) 일반화 오차 및 편향-분산 Trade off : 과대/과소적합 발생 문제
- 모델이 단순하면 Training Sample이 fitting을 잘 못해서 예측 오차가 커짐. 편향(Bias) 크고 분산(Variance) 적음.
- 모델이 복잡하면 Training Sample이 너무 fitting 해서 예측 오차가 커짐. 편향(Bias) 적고 분산(Variance) 커짐.
> 일반화 오차 = 편향^2 + 분산
> 과대적합을 막기 위해서는 : 훈련 데이터를 많이 확보하거나 모델 복잡도를 낮춤(변수 영향력 줄이거나, 차원을 축소시키거나, 파라미터 규제 적용하거나 등).
3. 머신러닝 모델의 평가지표
1) 회귀 모델
(1) RMSE (Root mean square error) : 제곱근(오차 제곱의 평균). 실제값과 예측값의 차이에 제곱을 하고 그 수의 평균을 찾음. 그 후 제곱근을 씌음
(2) R-square (결정계수) : 0이면 오차가 큰 상태, 1이면 오차가 거의 없는 상태.
(3) MAE (mean absolute error) : 오차 부호만 제거해서 평균한 값.
(4) MAPE (mean average percentage error) : 실제 값 대비 오차가 차지하는 비중이 평균 얼마인지 확인
2) 분류 모델
(0) 정오분류표 (confusion matrix)

(1) 정확도, 정분류율 (Accuracy) : (맞춘경우)/(전체경우)
(2) 정밀도 : (실제 Positive)/(예측 Positive 전체)
(3) 재현율 : (예측 Positive)/(실제 Positive 전체)
(4) ROC (Receiver operating characteristic) :

- AUC : ROC 곡선 아래 면적. 높을수록 좋은 모델. 1에 가까울 수록 좋음
4. 특성 공학
- 특성 공간의 차원을 축소해야 함. : 모델 해석력 향상, 훈련시간 단축, 차원의 저주 방지, 과적합에 의한 일반화 오차를 줄여 성능 향상.
1) 특성 선택 : 주어진 특성 변수 중 가장 좋은 특성변수만 선택
(1) filter : 랭킹 세워 가장 높은 몇가지 변수 선택
- 각 특성변수와 목표변수의 연관성을 1:1로 측정한 후, 목표변수를 잘 설명할 수 있는 특성 변수만을 선택하는 방식.
- t-test, chi-square test, information gain 등의 지표로 연관성을 파악함.
(2) wrapper : 모델에 fitting 해보고 결과로 판단
- 다양한 특성변수 조합에 대해 목표변수를 예측하기 위한 알고리즘을 훈련하고 cross-validation 등으로 훈련된 모델의 예측력을 평가.
- 여러 조합으로 학습->평가. 대표적인 방법으로 순차탐색법인 forward select, backward selection, stepwise selection 등이 있음.
(3) embedded : 모델이 직접 선택
- 처음부터 모델의 알고리즘 내에 최적화 변수를 선택할 수 있게 되어 있음.
- Ridge, Lasso, Elastic net 등이 있음
2) 특성 추출 (차원축소법 : 비지도학습)
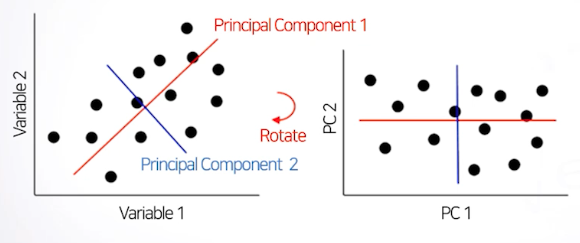
(1) 주성분 분석 (PCA) : 서로 연관된 변수들이 관찰되었을 때 변수들이 가진 정보들을 최대한 확보해서 새로운 변수를 생성하는 방법. 전체 변수 X1...Xk일 때 Y1...Yk까지 찾음. Y1이 가장 중요한 변수 (차원 축소).
- 자료에서 변동이 큰 축을 탐색함.
- 변수들에 담긴 정보 손실을 최소화 하며 차원을 축소함
- 서로 상관이 없거나 독립적인 새로운 변수인 주성분을 통해 데이터 해석을 용이하게 함.
- Y1은 데이터를 잘 설명하는 축이라면 Y2는 직교하는 축 중에 좌표성의 변동이 가장 커지는 축을 생성해 무관한 주성분을 만들어줌.
- 각 관찰치 별 주성분 점수는 Y1과 같은 주성분 좌표 축에서 값으로 재구성됨.
(2) 특성값 분해 (SVD) :
특이값 분해(SVD) - 공돌이의 수학정리노트
angeloyeo.github.io
- 정보가 많은 순서대로 m개만 이용하여 근사하는 경우 m계수 근사라고 함. m개만 이용해도 충분히 대표할 수 있는 값이 되는 경우임.
5. 비지도학습 - 군집분석 * 차원축소법도 비지도학습
1) 개요 : 대상들의 밀접한 유사성 또는 비유사성에 의하여 유사한 특성을 지닌 개체들을 몇 개의 군집(클러스터)으로 집단화하는 방법. 특이 군집 발견이나 결측값 보정 등에도 사용될 수 있음.
2) 계층적 군집분석 : 병합적 (개체간 거리 가까운 것 끼리 순차적 묶기), 분할적 (개체간 거리가 먼 것끼리 나눠 가기)
- 시간이 오래걸린다는 단점이 있음. 다른 군집분석의 군집 수를 정의하거나 미리 확인하고자 할 때 일부만 추출해서 보기도 하는 지표.
[거리 정의]
(1) 개체 간 거리 : 유클리디안 거리(물리적 거리), 맨해튼 거리, 민코우스키 거리
- 유클리디안 거리 : 좌표 평면간 두 점(a1,a2), (b1,b2)의 거리 sqrt((a1-b1)^2+(a2-b2)^2)
(2) 군집 간 거리 : 단일 연결법(최단 연결법), 완전 연결법(최장 연결법), 평균 연결법, 중심 연결법, ward 연결법 : 몇 가지를 시도해보고 덴드로그램 살펴보고 결정하는 것이 일반적
- 단일 연결법(<-> 완전 연결법) : 가장 가까운(<->먼) 요소들간 거리 측정
- 평균 연결법 : 모든 요소들 간 거리의 평균으로 정의
- 중심 연결법 : 모든 요소들의 중심을 정의하고 그 간의 거리로 정의
- ward 연결법 : (한 k군집의 중심과 그 군집의 개체간 거리의 제곱 합 =)SSEk.
(모든 SSEk의 합) + sum of squares = (군집을 고려하지 않고 모든 개체간의 중심 지점의 SSE)
sum of squares이 증가한 정도가 클 수록 멀다고 정의. 작을수록 가깝다고 정의.
(2) 덴드로그램 : 각 개체 별 클러스터링 과정을 시각화 한 그림(그래프)
3) 비계층적 군집분석
(1) K-means 군집분석 : 사전 결정된 k 만큼 군집 형성. 계산량 적고 대용령에 빠르게 처리함. 초기 군집 중심이 어디냐에 따라서 결과가 바뀔 수 있음. 잡음, 이상치 영향을 많이 받음
(2) k-means의 알고리즘 : k개 초기 군집으로 나눈다 -> 각 군집 중심을 계산하고 가장 가까운 군집에 할당시킴 -> 새로운 개체를 받아들이거나 잃은 군집의 중심을 다시 계산 -> 반복
(3) 군집 수 결정 : 오차제곱합(SSE, sum of squared error) : 군집수 k에 따른 SSE 변화를 시각화하고 SSE가 급격히 감소하다가 완만해지는 지점의 k를 적정 군집수로 판단.
6. 지도학습 - 회귀분석 : 독립변수-종속변수 간 함수적 관련성을 규명하기 위해 수학적 모형을 가정하고, 이 모형을 측정된 자료로부터 통계적으로 추정하는 분석 방법.
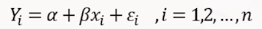
1) 단순선형회귀분석
(1) 정의 : 독립변수가 1개. 오차항들은 서로 독립인 확률변수(정규, 등분산, 독립가정)
(2) 모수 의미 : α(알파), β(베타) 회귀계수, ε(엡실론) 오차항
(3) 모수 추정법(최소제곱법) : 수직거리 제곱합 SS(α, β)이 최소가 되도록 하는 α, β를 추정하는 방법
(4) 모수에 관한 가설 검정(t 검정)
- 귀무가설 H0 : β(x의 계수)가 0이면 : X는 Y를 설명할 수 없음(전혀 관계없음)
- 대립가설 H1 : β가 0이 아니면 : X는 Y를 설명할 수 있음(관계 있음)
* T통계량의 위치를 파악하고 설정한 유의수준을 넘어가면 기각.
* p-value 값이 0.05 이하면 유의성이 검증됨.
(5) 적합도(R-square)
- 제곱합 : SST(yi의 변동) = SSR(모형으로 설명되는 변동) + SSE(모형으로 설명되지 않는 변동)
- R^2 = SSR/SST = 모형으로 설명되는 변동/전체 Y 변동 = 1 - SSE/SST = 1 - (모형으로 설명되지 않는 변동/전체 Y 변동) = 두 변수간의 상관계수 r의 제곱과 같음 ( = 선 주변에 얼마나 많이 모여있는가?) : 0 <= R^2 <= 1
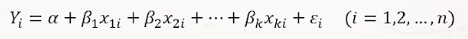
2) 다중선형회귀분석
(1) 정의 : 독립변수가 2개 이상
(2) 모수 의미 : α(알파), β₁..(베타) 회귀계수, ε(엡실론) 오차항
(3) 모수 추정법 = 최소제곱법
(4) 적합도(R-square) : 단순회귀와 동일한 방식
* 범주형 독립변수가 포함된 회귀모형 : 더미변수 기법 사용
(5) 변수선택 (특성선택 중 wrapper) : forward select, backward selection, stepwise selection
- 전진선택법 : 절편만 있는 모델에서 출발해서 (*부분 F 검정을 통해 검증해서 : β가 0에 먼 경우) 가장 중요한 변수를 하나씩 추가하는 방식. 한번 선택된 변수는 제거되지 않는 단점이 있음.
- 후진제거법 : 전체 선택으로 출발해서 (부분 F 검정을 통해 검증해서 : β가 0에 가까운 경우) 가장 중요하지 않은 변수를 하나씩 제거하는 방식. 한번 제거된 변수는 다시 선택되지 않는 단점이 있음
- 단계별 방법 : 절편만 있는 모델에서 출발해서 (부분 F 검정을 통해 검증해서 : β가 0에 먼 경우) 중요한 변수부터 추가하고 모델에 포함되어 있는 변수중에서 가장 중요하지 않은 변수를 제거함. 선택과 제거를 매 단계에 고민함.
* 모형선택의 기준 : 수정된 결정계수 : R^2 = 1 - [{SSE / (n-k-1)} / {SST / (n-1)}] : 변수 개수가 적은거보다 지금이 더 낫나?
(6) 잔차(=오차에 대한 추정치)분석
- 오차 가정 : 정규성, 등분산성, 독립성
- 가정 위반시 : 정규성 위반 -> 변수변환, 등분산성 위방 -> 가중최소제곱회귀, 독립성 위반 -> 시계열 분석
- 잔차 분석 방법
* 검정을 통한 방법
* 그래프를 통한 시각적 방법 : 정규성 -> 히스토그램, QQ플롯 | 등분산성, 독립성 -> 잔차산점도(잔차가 함수관계 패턴을 보이는 경우는 선형관계에도 문제가 있을 수 있음)
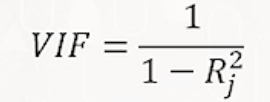
(7) 다중공선성 : 독립수준 간에 강한 상관관계가 (회귀계수 추정에) 부정적 영향을 미치는 현상.
- VIF 계수 도출(오른쪽 이미지). Rj^2 (알고싶은 변수인 Xj를 제외한 독립변수에 대한 R square 점수)
* VIF 5 (Rj^2 80%) or 10 (Rj^2 90%) 이상 인 경우 다중공선성 문제가 심각하다고 판단.
- 해결책 : 변수선택으로 중복된 변수 제거, 주성분 분석 등을 이용해 중복된 변수 변환해서 새로운 변수 생성. 릿지, 라쏘 등으로 중복된 변수 영향력 통제
3) 규제가 있는 선형회귀모델
: 모델 과적합 방지를 위해 규제 (릿지, 라쏘, 엘라스틱넷) 파라미터가 너무 커지지 않게 하거나 중요하지 않은/중복된 변수 영향력 줄이기
- 규제 방법 : 선형회귀 모형에서는 모델의 가중치(회귀계수)를 제한(penalty)하는 방법을 사용함. * Lp norm = ᴾ√(Σ | β𝚓 | ᴾ )
(1) 릿지 : P=2 (L2 norm) : 비용함수에 규제항 𝝀*L2 norm이 추가된 선형 회귀 모형.
- 𝝀(규제정도를 결정하는 하이퍼파라미터) : 크면 규제 많음(회귀계수 추정치 작아짐), 0이면 일반 선형회귀모델과 동일한 결과. cross-validation으로 적절한 𝝀 찾기.
- 𝝀에 1:1로 대응하는 하나의 𝑡가 존재. 𝑡는 작을수록 규제를 많이한다.
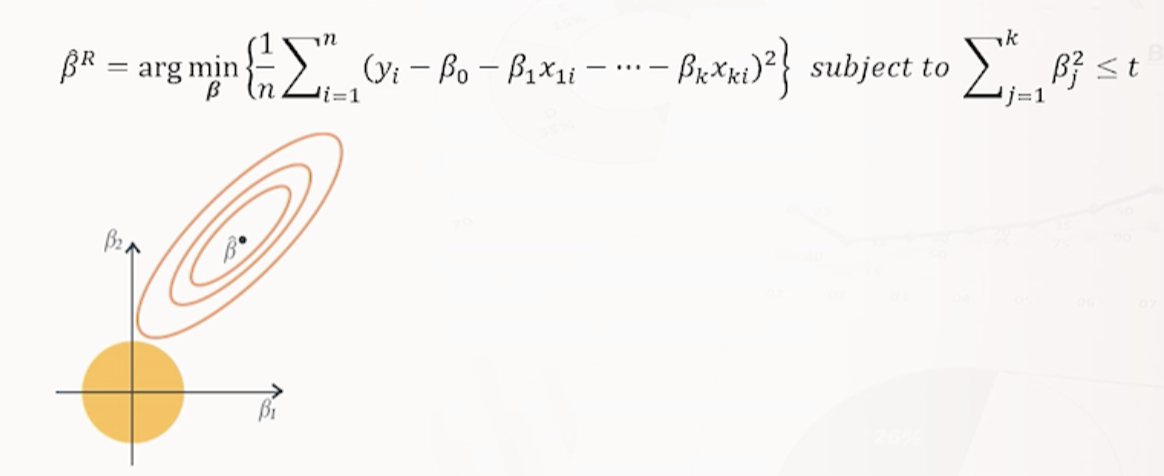
* 릿지회귀의 경우 제약범위가 원 형태이기 때문에 Bj는 0이 되지 않고 전반적으로 줄어드는 경향이 있음
(2) 라쏘 : P=1 (L1 norm) : 비용함수에 규제항 𝝀*L1 norm이 추가된 선형 회귀 모형
- 𝝀 : 크면 규제 많음(위와 동일)
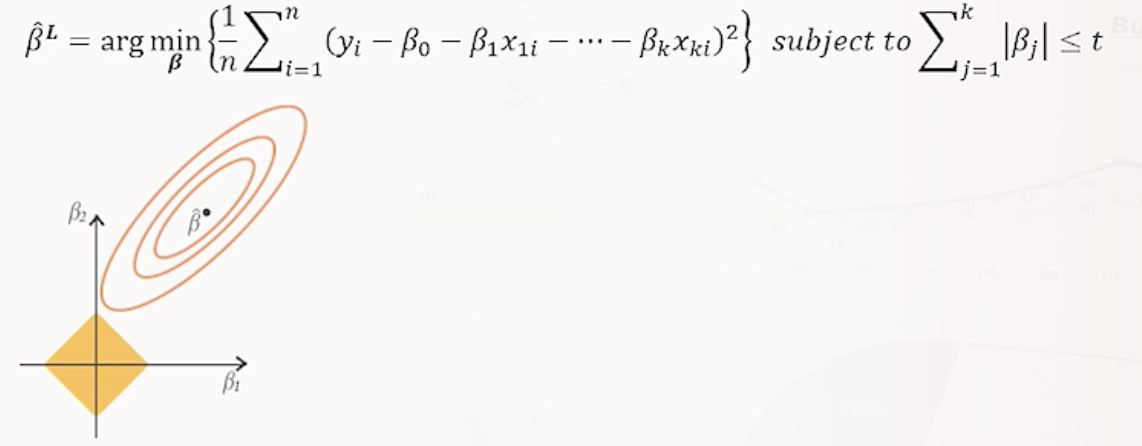
* 라쏘회귀의 경우 제약범위가 각진 형태이기 때문에 Bj 일부가 0이 되서 영향력이 사라지는 경향이 있음.
(3) 엘라스틱넷 : 릿지 + 라쏘 : L1규제와 L2규제를 혼합함. 두 모델의 장점 모두 가짐. 다만 추정에는 복잡할 수 있음.
7. 지도학습 - 분류분석
1) 로지스틱 회귀 : 종속변수가 범주형인 데이터인 경우에 사용.
- 새로운 설명변수 값이 주어질 때, 반응변수의 각 범주에 속할 확률이 얼마인지 추정하고 추정 확률을 분류 기준 값(threshold, cut-off)에 따라 분류하는 모형
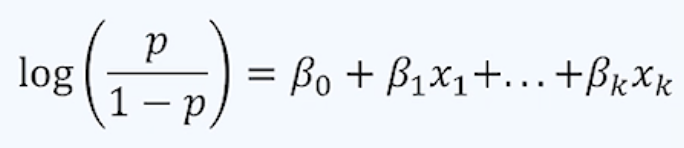
(1) 이항 로지스틱 회귀모형 : 이진형 값을 가지는 반응변수를 회귀식의 형태로 예측하는 모형
- 로그오즈(오른쪽 이미지의 좌항) : 관심있는 사건은 그렇지 않은 사건의 확률의 몇배?
* 왜 로그오즈 사용? 확률 p는 0~1. 변환하지 않은 경우 (-∞, ∞) 범위를 가지는 독립변수 선형함수 vs (0~1) 범위로 범위 상이함.
* p = 1/2 (반반 확률일때) -> 오즈 P/(1-P) = 1
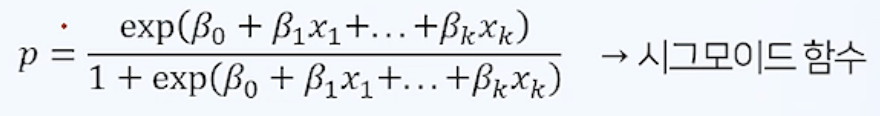
- 설명변수가 1개인 경우 아래와 같은 곡선형태를 가짐. p는 0~1사이값. p가 0일때 x = -∞, p가 1일때 x = ∞
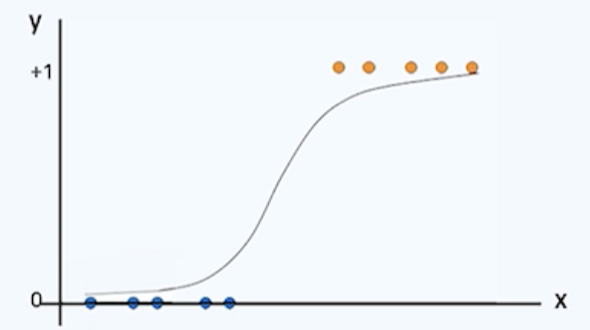
- 추정 및 예측 : 최대우도추정법, 경사하강법 등 이용해서 가장 적합한 곡선 함수 추정 -> 새로운 자료 주어질때 p값 도출 -> threshold 기준점보다 크다면 1, 작다면 0으로 판단
- 분리경계면 : X라는 특성변수들만의 공간에서 어느 점을 기준으로 Y의 값을 예측하는지 표현한 경계면
- 오즈비 : 나머지 변수는 모두 고정시킨 상태에서 한 변수 X1만 1만큼 증가시켰을 때 변화하는 오즈의 비율(상수값) = ℯ ^ (β1)
* 로지스틱 회귀와의 관계 : x1만 1만큼 증가하면 오즈는 exp(β1)배 변화함 : β1가 양수면 양의 상관관계, β1가 음수면 음의 상관관계
(2) 나이브베이즈 : 생성 모델의 일종으로 활용.
* 목표변수 Y가 2개를 가질때 특성변수 X의 값을 이용해 Y범주를 예측하는 문제
- (조건부확률) P[C1|x] > P[C2|x] 이면 C1으로 분류하고 그렇지 않으면 C2로 분류. -> 베이즈 정리를 이용 P[x|C1]*P[C1] > P[x|C2]*P[C2]
* 목표변수 Y가 n개를 가질때 ...(각 특성변수들이 모두 독립이라고 가정할 때 -> 너무 나이브한 가정..)
- 장점 : 연산속도 빠름. 학습 데이터 양 적어도 좋은 성능. 다양한 텍스트 분류나 추천 등에 활용됨.
- 단점 : 특정 빈도가 0인 경우나 Underflow 문제가 있음. 모든 독립변수가 독립이라는 가정이 너무 단순함.
(3) KNN (K-Nearest-Neighbor)
- 가장 가까운 k개의 데이터를 바탕으로 예측하기 때문에 K의 결정이 매우 중요한 문제임.
* k가 작으면 이상점 등 노이즈에 민감하게 반응하는 과적합 문제 발생.
* k가 크면 자료 패턴을 파악하기 어려워 예측 성능이 저하됨.
- 거리 측정 방식 : 유클리디안 거리(제곱하고 제곱근), 맨해튼 거리(절대값), 민코우스키 거리(절대값 제곱하고 제곱근)
* 자료 스케일이 다른 경우 (스케일링) : 표준화 변환 (Z score) 또는 min-max 변환
8. 의사결정나무
'데이터 어쩌구 > ML DL 공부' 카테고리의 다른 글
| [ProDS] 통계 이론 및 데이터 시각화 (0) | 2022.03.15 |
|---|
